Итак, я постарался раскрыть понятие параметрического проектирования. Настало время углубиться в методологию. Рассмотрим метод изнутри и изучим то, чем же он оперирует.
Метод имеет в основе логику, отличную от логики методов прошлых поколений. Он оперирует иными понятиями и, таким образом, заставляет мыслить совершенно иными категориями. Здесь полностью меняется теория организации пространства.
Понятия и принципы этого метода сложны для понимания архитектора и дизайнера, обучавшегося на нашей с вами родине. Архитектурная школа прошлых лет основана на изучении статичных систем организации пространства. Для нашего брата архитектура с детства была “застывшей музыкой”. Этот факт является одной из главных причин столь заторможенного развития архитектуры в России. Собственно российская архитектурная школа на данный момент вообще остановилась в своем развитии и занимается попытками “подогнать” мировые стандарты эстетики под свои, уже ставшие историей, нецелесообразные методы.
Поговорим лишь о двух, наиболее важных понятиях. Динамическая система и аттрактор. Остальные определения логически вытекают из них и, на данном этапе понимания метода, не требуются (ведь я пытаюсь рассказать о методе человеку, который воспитывался в вышеописанной среде).
Динамическая система — математическая абстракция, предназначенная для описания и изучения систем, эволюционирующих с течением времени.
Динамическая система представляет собой математическую модель некоторого объекта, процесса или явления.
Динамическая система может быть представлена в виде «чёрного ящика» с «входами» и «выходами». «Входы» представляют собой внешние (например, управляющие) воздействия на систему, а «выходы» — ответную реакцию системы (её поведение). При таком подходе, основная задача — это поиск управляющих воздействий, обеспечивающих требуемое поведение системы. (Вам ничего не напоминает?=)
Это наиболее полное определение, из тех что я нашел. Источник - Малинецкий Г. Г., Потапов А. Б., Подлазов А. В. Нелинейная динамика: подходы, результаты, надежды. М.: УРСС, 2006.
Интересно то, как определения из разных областей науки постепенно проникают друг в друга и в нашем случае из математики в архитектуру.
Динамическая система также может быть представлена как система, обладающая состоянием. При таком подходе, динамическая система описывает (в целом) динамику некоторого процесса, а именно: процесс перехода системы из одного состояния в другое.
Фазовое пространство системы – совокупность всех допустимых состояний динамической системы. Таким образом, динамическая система характеризуется своим начальным состоянием и законом, по которому система переходит из начального состояние в другое.
Аттрактор – совокупность внутренних и внешних условий, способствующих "выбору" самоорганизующейся системой одного из вариантов устойчивого развития. Другое определение – идеальное конечное состояние, к которому стремится система в своем развитии. Пространство внутри аттрактора, в котором каждая частица (система), туда попавшая, постепенно смещается в заданном направлении, называют "зоной аттрактора".
Пример: перераспределение железных опилок в поле действия магнита с ориентацией их на полюса. Аттракторы - структуры – то есть реальные формирования объективного мира, которые обладают набором оптимальных характеристик и к обретению устройства которых стремятся структуры менее совершенные, не выдерживающие давления со стороны среды в конкуренции с другими, себе подобными. (Очень сильно перекликается с теорией эволюции Дарвина, стоит лишь подставить вместо слова “структура” слово “вид”)
Аттрактор – совокупность внутренних и внешних условий, способствующих "выбору" самоорганизующейся системой одного из вариантов устойчивого развития. Другое определение – идеальное конечное состояние, к которому стремится система в своем развитии. Пространство внутри аттрактора, в котором каждая частица (система), туда попавшая, постепенно смещается в заданном направлении, называют "зоной аттрактора".
Пример: перераспределение железных опилок в поле действия магнита с ориентацией их на полюса. Аттракторы - структуры – то есть реальные формирования объективного мира, которые обладают набором оптимальных характеристик и к обретению устройства которых стремятся структуры менее совершенные, не выдерживающие давления со стороны среды в конкуренции с другими, себе подобными. (Очень сильно перекликается с теорией эволюции Дарвина, стоит лишь подставить вместо слова “структура” слово “вид”)
Для выяснения сущности этих понятий рассмотрим динамическую систему. Понятие динамической системы состоит из двух частей: понятия состояния (существенной информации о системе) и динамики (правила, описывающего эволюцию системы во времени). Эволюцию можно наблюдать в пространстве состояний (или фазовом пространстве), абстрактном пространстве, в котором координатами служат компоненты состояния. При этом координаты выбираются в зависимости от контекста. В случае механической системы это могут быть положение и скорость, в случае экологической модели – популяции различных биологических видов.
Точка или множество точек (например, петля, цикл), к которому стремится прийти система, называется аттрактором (от лат. attractio – притягиваю). Другими словами, аттрактор – это точка или некоторое множество точек, к которому стремится динамическая система с течением времени, как бы «забывая» начальные условия. Действительно, каковы бы не были начальные значения переменных системы, по мере развития динамического процесса, они будут стремиться к одним и тем же значениям или одним и тем же множествам значений – аттракторам. Таким образом, аттракторы – это геометрические структуры, характеризующие поведение в фазовом пространстве по прошествии длительного времени.
Одна и та же система может иметь несколько аттракторов. Если это так, то разные начальные условия могут привести к разным аттракторам. Множество точек, приводящих к некоторому аттрактору, называется его областью притяжения. Система с маятником имеет две такие области: при небольшом смещении маятника от точки покоя он возвращается в эту точку, однако при большом отклонении часы начинают тикать и маятник совершает стабильные колебания.
Одна и та же система может иметь несколько аттракторов. Если это так, то разные начальные условия могут привести к разным аттракторам. Множество точек, приводящих к некоторому аттрактору, называется его областью притяжения. Система с маятником имеет две такие области: при небольшом смещении маятника от точки покоя он возвращается в эту точку, однако при большом отклонении часы начинают тикать и маятник совершает стабильные колебания.
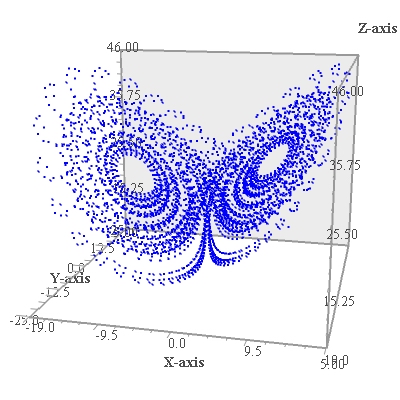
Свойства аттракторов задаются набором траекторий в пространстве n переменных состояния, которые зависят от времени как от параметра. В обычном аттракторе эти траектории простые (точка, окружность, эллипс и т.п.). Но ряд явлений сопровождается появлением траекторий запутанных, не похожих ни на точки, ни на кривые, ни на поверхности, имеющих вид «спутанных клубков», многослойных поверхностей. Такие аттракторы получили названия «странных аттракторов». Странность состоит в том, что, попав в область странного аттрактора, точка, соответствующая состоянию системы будет «блуждать» там и только через большой промежуток времени приблизится к какой-либо точке аттрактора. Поведение системы выглядит при этом хаотическим, а ее дальнейшее поведение сильно зависит от начальных условий.
(Уфимский Государственный Авиационный Технический Университет. Такую основу представляет собой курс лекций по Концепции Современного Естествознания.)
- Примером может служить Аттрактор Лоренца, который описан на множестве языков программирования, достаточно заглянуть на WIKI =)
Таким образом мы подходим к пониманию термина “морфинг” (morphing). Постепенное превращение объекта с одним набором характеристик в объект с совершенно другим набором.
Объект проходит N-ое количество фазовых состояний, в процессе чего постепенно теряет начальные характеристики и приобретает новые. Процесс может быть не линеен. А зависимость представлять из себя любой закон: математический, физический или биологический. Кроме того, процесс развития может быть не линеен и не постоянен.
Объект проходит N-ое количество фазовых состояний, в процессе чего постепенно теряет начальные характеристики и приобретает новые. Процесс может быть не линеен. А зависимость представлять из себя любой закон: математический, физический или биологический. Кроме того, процесс развития может быть не линеен и не постоянен.
![[POPOV NIKITA] :. PARAMETRIC SOMETHING .:](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEh1MAL5q7hhdAg6jkEYbEZ2dD6AdzmMZU7tmZ0tt0ebub-jno-0KAfFKyK3EQlbnybK7LXS1bE1dIsWeB8M0m2GjKGj32mxrfvyAZ7Swtv6d2uft21HUbm8Gj9kAbDnzWzO8iHZDMebPF8/s968/blog_topic.jpg)